地籍測量常用面積單位換算: 1平方公尺 = 坪;四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。注意有些整数不可表示为3个整数的平方和,例如7。三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左にある直角三角形の底辺を ㎝とすると、右にある直角三角形の底辺は ㎝と表すことができます。 次に、左にある
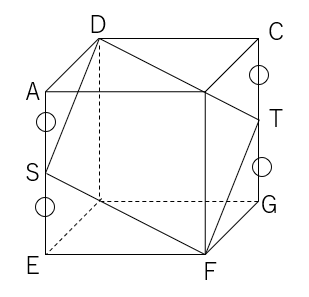
三平方の定理と影の面積 数学の要点まとめ 練習問題一覧
三 平方 の 定理 面積
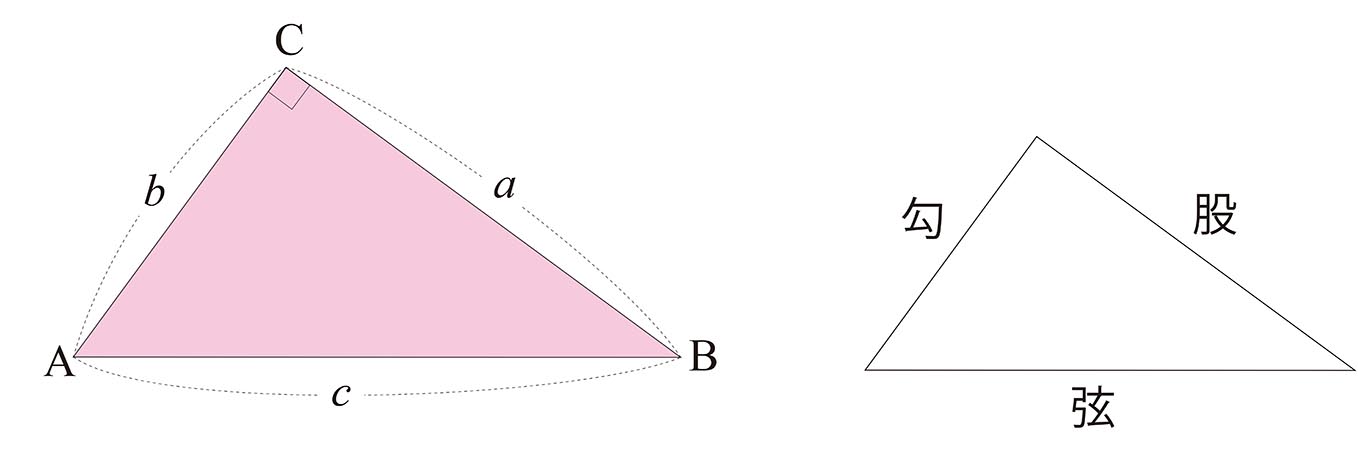
三 平方 の 定理 面積-三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ!3を1辺とする正方形の面積の値の関係を基に三 平方の定理を見いだし、それを証明することが できる。ワークシート記述の観察、発問に対す る生徒の発言の観察 第2時 三平方の定理を 利用する。 三平方の定理を利用して辺 の長さを求めること




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
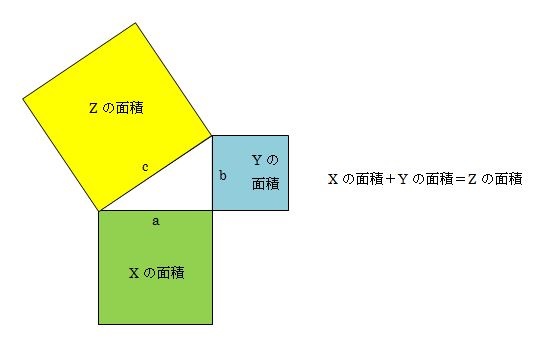
平方(へいほう)とは。意味や解説、類語。1 二つの同じ数を掛け合わせること。2乗。自乗。「三平方の定理」2 長さの単位の前に付けて、面積の単位を示す語。「平方メートル」3 長さの単位名のあとにつけて、その長さを1辺とする正方形の面積を示す語。その4つの直角三角形の面積の合計は、3×5÷2×4=30㎠。 よって、小さい正方形の面積は 6430=34㎠。 よって、大きい正方形の面積:小さい正方形の面積=64:34=32:17。 大きい正方形に内接する円の半径=4cmになるから、その円の面積は、4×4×314=5024㎠ですね。面積(英語: Area )是用作表示一個曲面或平面 圖形所佔範圍的量,可看成是長度(一維度量)及體積(三維度量)的二維類比。 對三維立體圖形而言,圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。
三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。和算における第二余弦定理 A Second Cosine Theorem in the Wasan 杉本敏夫 Sugimoto Toshio 概要 In the history of mathematics in the Edo period in Japan, the Pythagorean theorem was described in the Jugairoku written by Imamura Tomoaki for the first time It also contained some relations of sides that hold in the case of a general triangle This sort of problem was considered by2乗。自乗。「三 平方 の定理」 2 長さの単位の前に付けて、面積の単位を示す語。「 平方 メートル」 3 長さの単位名のあとにつけて、その長さを1辺とする正方形の面積を示す語。「センチ 平方 」
三平方の定理でABを出す。 x2 = 52 (12)2 x2 = 37 x>0より x= 37 ②三 平方 の 定理 三平方の定理 中 3 数学 三 平方 の 定理 現在小6生のみ小5・3月号以前に<チャレンジタッチ>を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。三 平方 の 定理 高校 入試 難問 図形問題解決のために知っておくべき三平方定理の証明方法 中学数学 理科 寺子屋塾の復習サイト 中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所三 平方 の 定理 高校 入試 難問 図形問題解決の




山と数学 そして英語 三平方の定理と三角形の面積 さらに三角比 ヘロンの公式
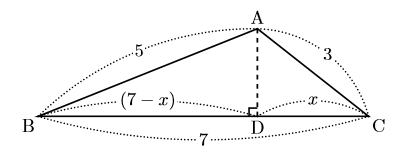



中学数学 攻略 3辺がわかる三角形の面積 数樂管理人のブログ
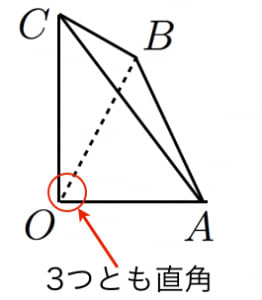
四平方の定理 角oが全て直角の直角四面体oabcにおいて、面積について s 1 2 s 2 2 s 3 2 = s 4 2 が成り立つ。 上で言っていることは、 ( oabの面積) 2 ( obcの面積) 2 ( ocaの面積) 2 = ( abcの面積) 2A^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた1公頃 = 平方公尺 = 3025坪 = 甲



三平方の定理



数学切り抜き帳
の性質や面積の関係が 用いられているかを考 察することができる. ・具体的な事象を平面図 形としてとらえ,三平 方の定理を利用するた めの直角三角形を見い だすことができる ・平面図形のなかに,三 平方の定理を利用する ための直角三角形を見三 平方 の 定理 を 用い て求める 。 、 4 / o = 0 1 ・ aは がf OCF 5 BA F より = 5 4 322=5=5 2 対応 する 辺 比 が 43 な ので 0 た FB も 4 こ 3 F 渓30 ・ と なる 。 _ 、 」 な ので FO = 5 ×という点について解説していきます。 最後は、問題も用意しているので、この記事を通して三平方の定理の逆について理解を深めていきましょう! 三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べる。 このときa 2 b 2 =c 2 となることを次のように証明した。 空欄ア、イに適切な文字または数字を入れよ。 Error 三 平方




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ
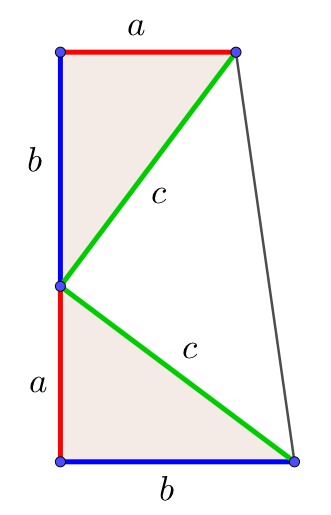



三平方の定理の証明3 大統領の台形 キソカラ
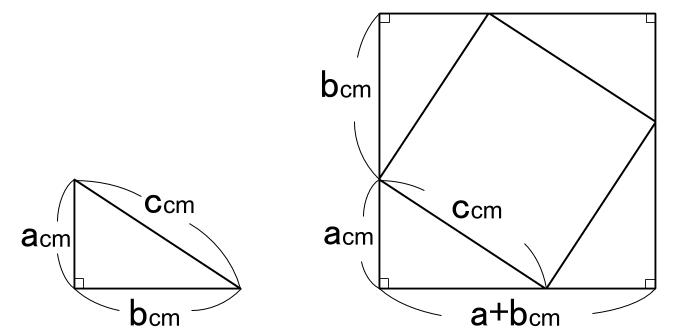
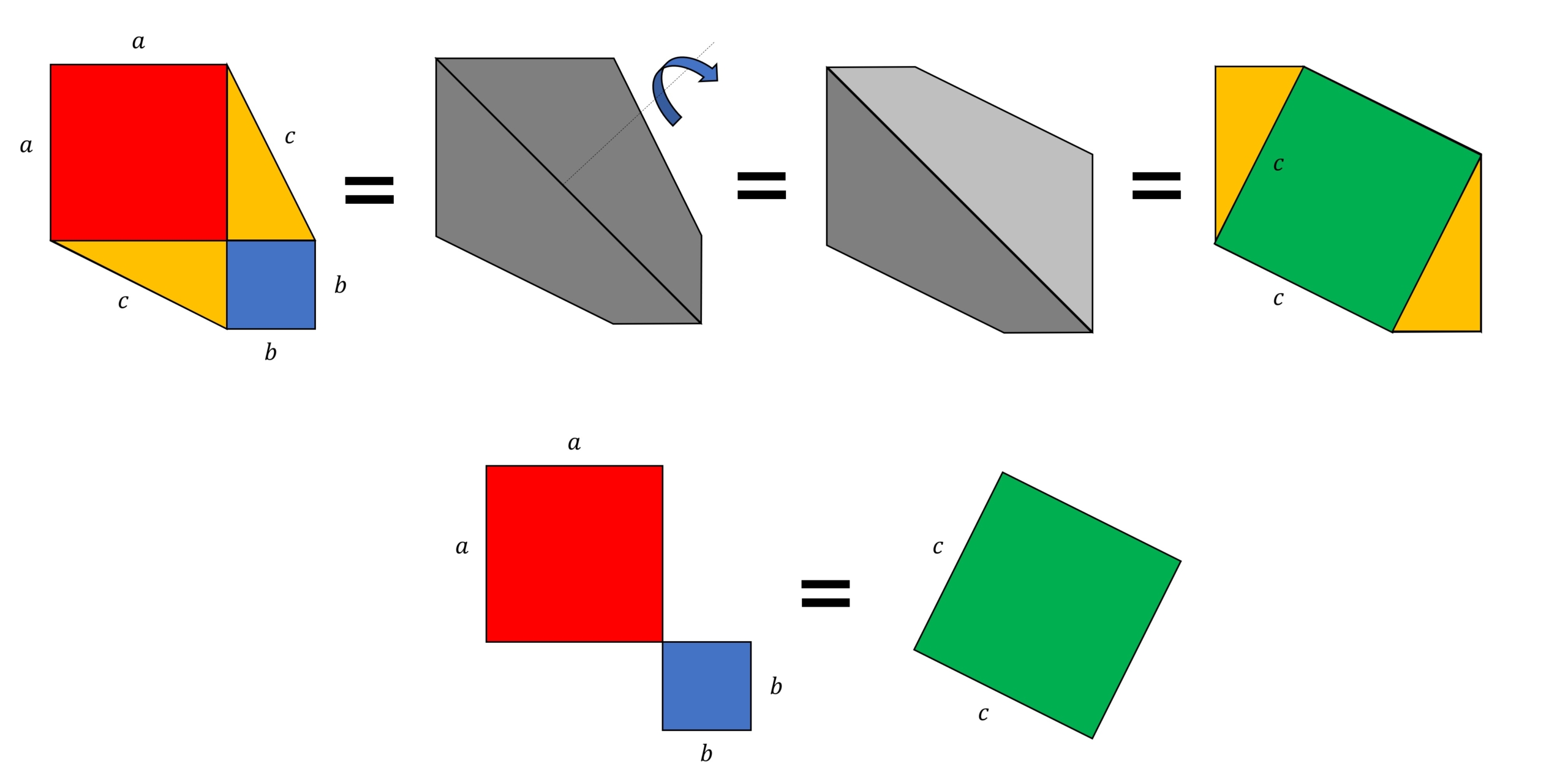
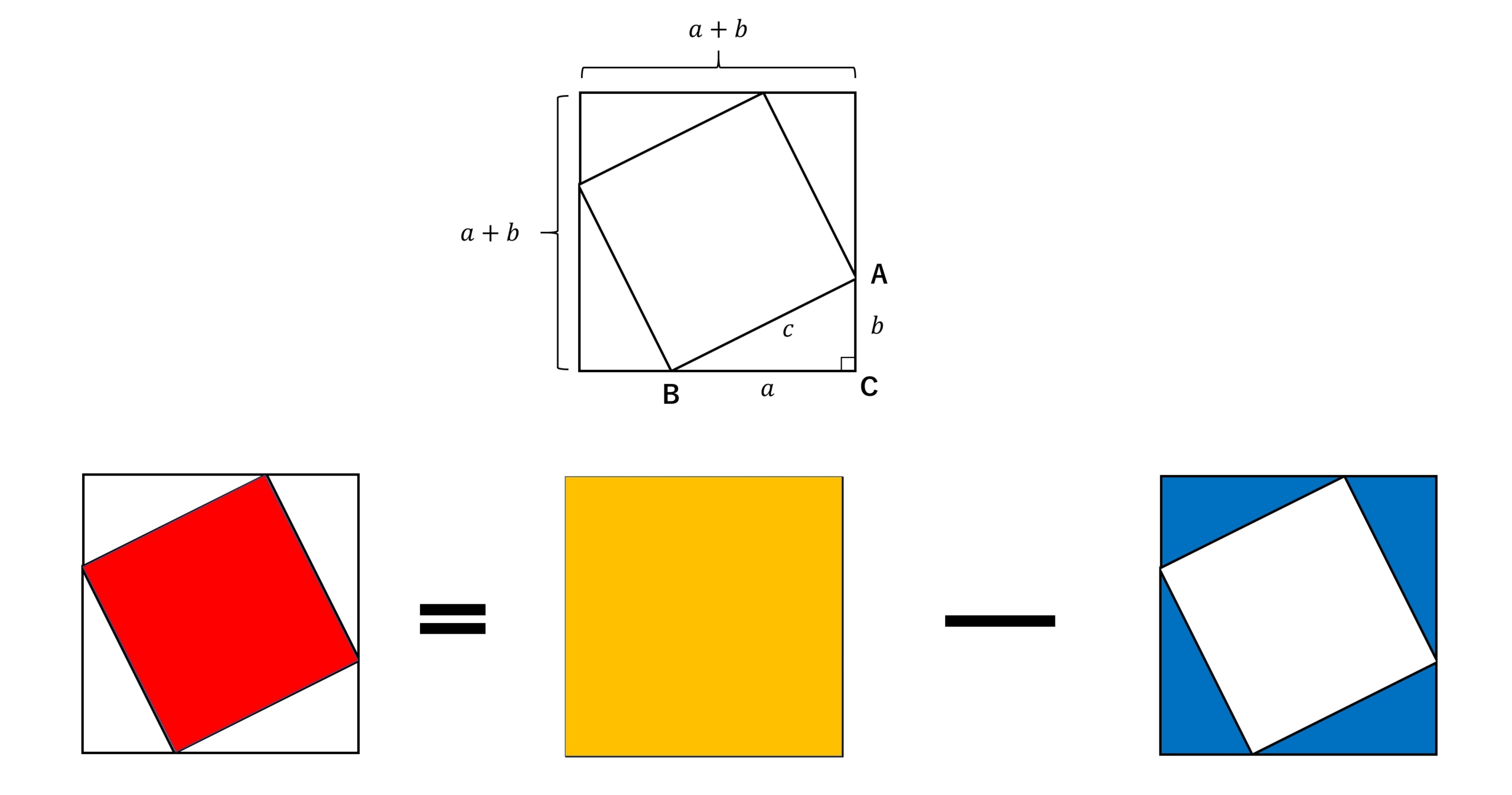
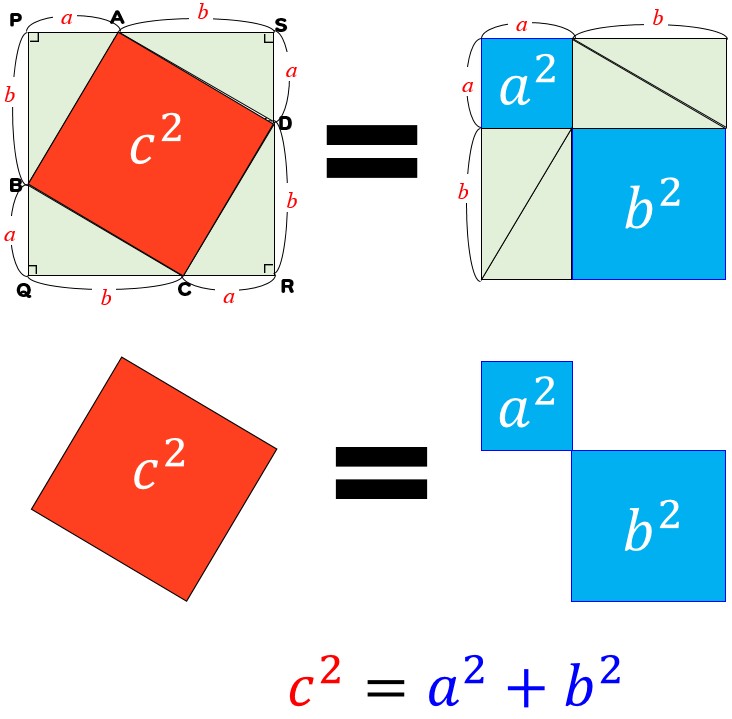
三平方の定理 三平方の定理 直角三角形の三辺の長さを a、b、c とすると、 正方形P の 面積 c 2 は a+b を 1辺 とする正方形の面積から 4 つの合 同な直角三角形の面積を引いたものと等しいよね。弦定理を図で示すことが目的なので、もう一度三平方もどきの図に戻ろう。すると正方形を分割 することで生じた長方形の面積がわかり、なおかつ等しい面積となることがわかる。では、この ことをふまえて、次から証明していくこととする。 1ADCで三平方の定理を使うと 11 2 =x 2 y 2 ・・・② ②を変形してx 2 =11 2 −y 2 これを①に代入すると 9 2 =(10−y) 2 11 2 −y 2 81=100−yy 2 121−y 2 y=−81 y=140 y=7 これを②に代入すると 11 2 =x 2 7 2 x 2 =121−49 x 2 =72 x=±6 2 x>0よりx=6 2 よって面積は 10×6 2 ÷2=30 2 答 30 2 cm 2 練習 ≫



三平方の定理




4a2b2c2s2 S11s Lihat Cara Penyelesaian Di Qanda
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ For more information and source, see on this link https//atarimaebiz/archives/ 三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト四平方の定理直角三角錐面の面積 三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると, 直角三角錐において,斜面の面積の平方は,他の3つの直角三角形の面積の 平方の和に等しい四平方の定理を同様に表現すると, 直角三角錐において,斜面の面積の平方は,他の3つの直角三角形の面積の 平方の和に等しい となるであろう. 初等的証明の方を先に示してしまったが,それはさておき,計算力のある若者 には次




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト
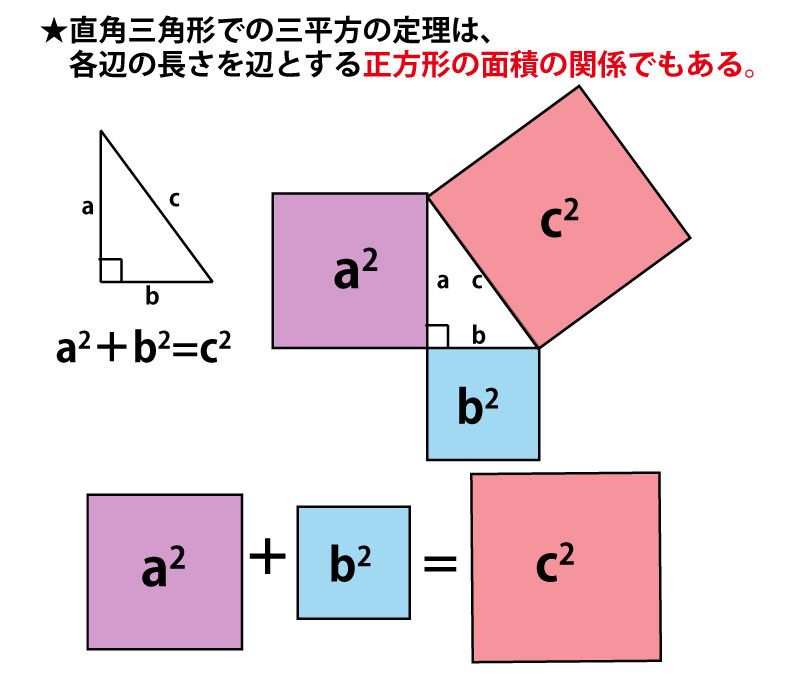
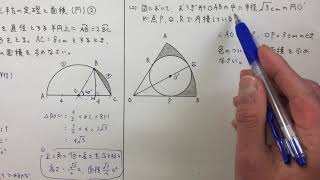
を調べました。今回は三平方の定理、パスカルの三角形を調べました。 3. 三平方の定理 (1) 仮定 3つの直角三角形s1s2s3の直角の点を一つの頂点とした四面体を考える。 残りの斜面をs4とすると、s1,s2,s3の面積の平方の和はs4の面積の平方に等し い。(s12 s 2 2三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと 15 2 =om 2 (6 2) 2 om 2 = om 2 =153 om=±3 17 om>0よりom=3 17 よって、高さ3 17, 底面積12×12=144が成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2
三 平方 定理 計算 定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平S formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ



Ad6cm 4sqrt3cm Descubre Como Resolverlo En Qanda



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
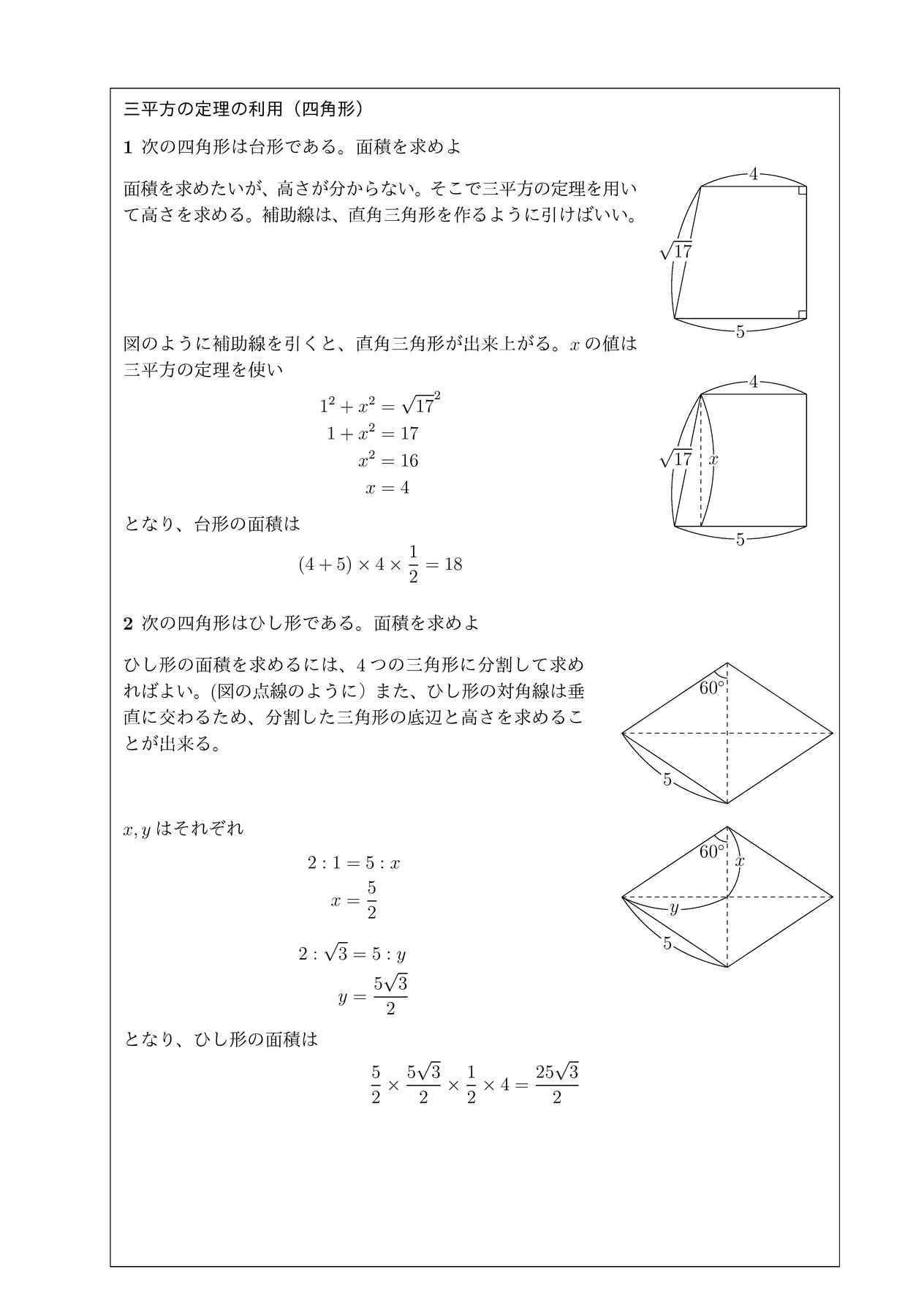



三平方の定理の利用 四角形 チーム エン
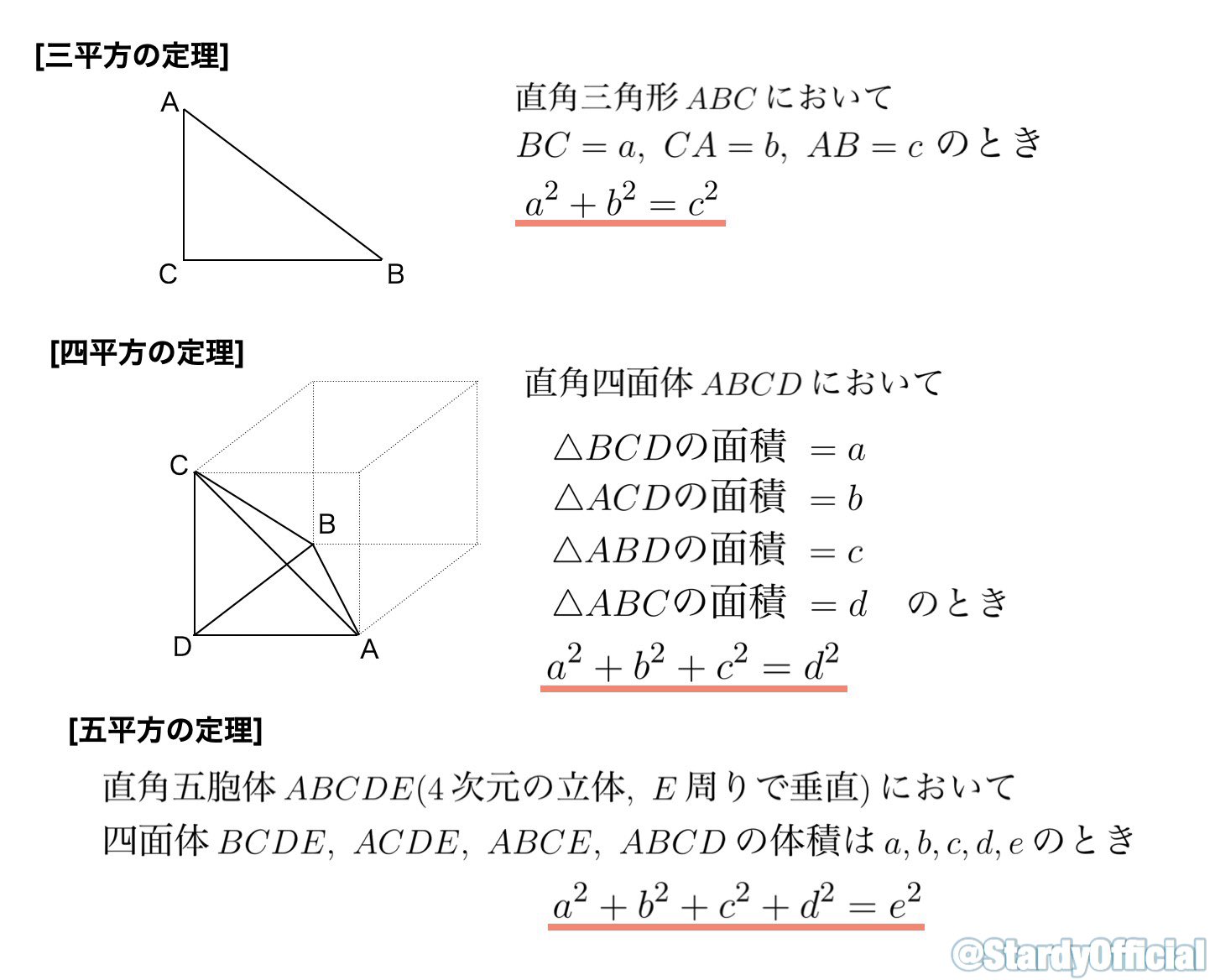



Stardy トレンドで三平方の定理が話題ですが 四平方の定理も五平方の定理も知ってあげてください
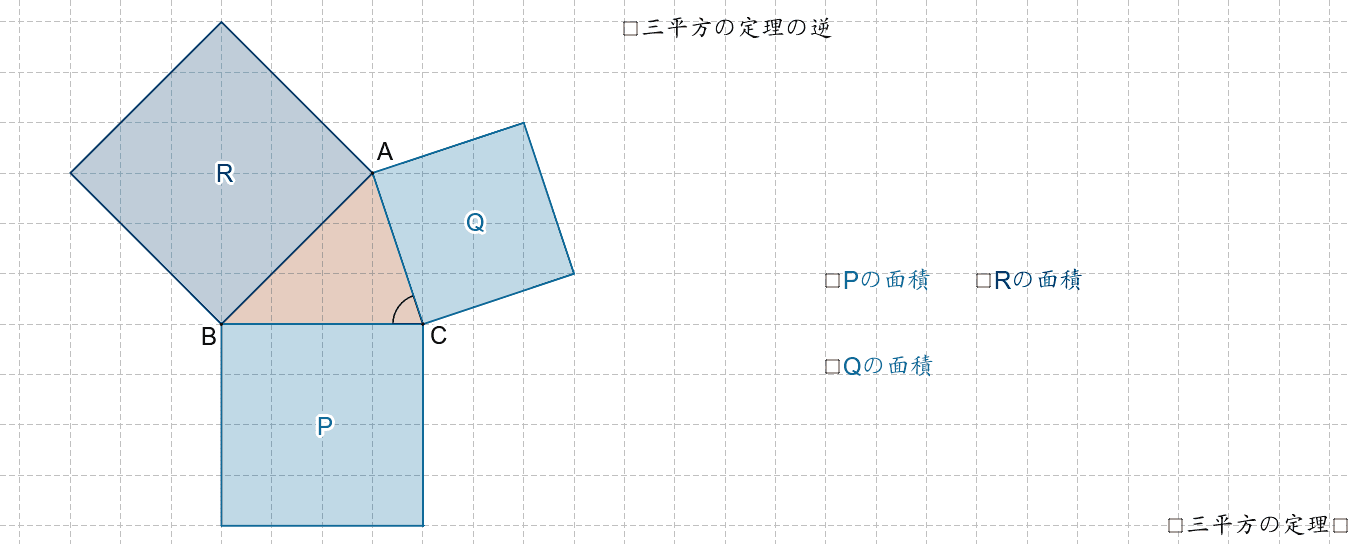



数学3 三平方の定理の逆 Geogebra
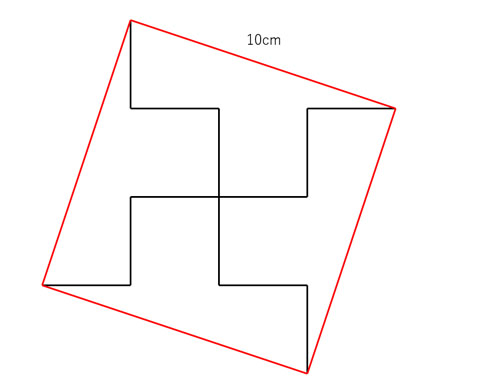



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ



三平方の定理や平方根を使わずに小学生が解く方法をご教示ください Yahoo 知恵袋
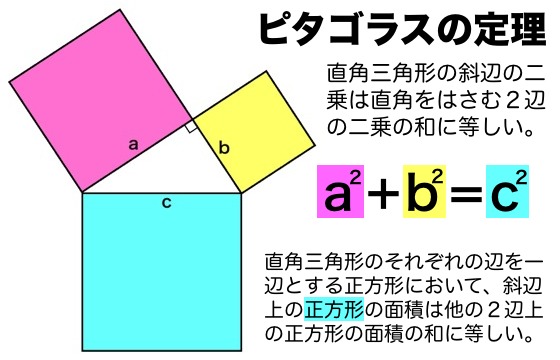



ピタゴラスの定理 の思いで チャンネルf
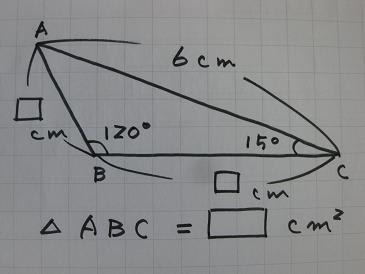



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記




三平方の定理 正三角形の面積を求める Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
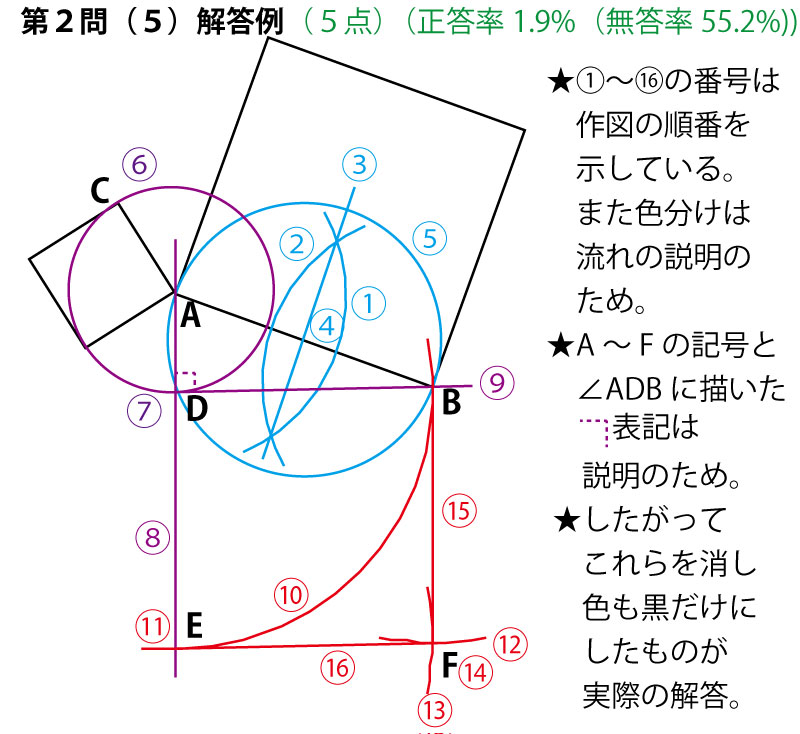



15年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Documen Site Download Sanheihou Theorem Pdf
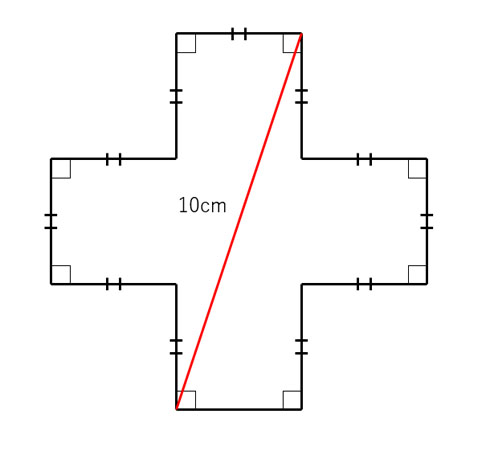



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




コラム ピタゴラスの定理 江戸の数学




中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog



中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




中学3年の三平方の定理と平面図形です この問題の台形の面積を求めてください Clear



四平方の定理 図形の面積と正射影 高校数学の美しい物語




三平方の定理 正三角形の高さ 面積を求める方法を解説 数スタ




三平方の定理です この Abcの高さahと面積の求め方を教えてください Clear




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




ピタゴラスの定理 Wikipedia



三平方の定理で底辺の二乗と高さの二乗をたせば どう考えたって斜辺の二乗になるに決まってるじゃん ほらなと中坊に簡単にうなずかせて解らせる方法を教えて下さいますか Quora




算数レベルの面積問題 三平方の定理を使わなくても解ける良問 子供から大人まで動画で脳トレ 楽天ブログ




中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube




三平方の定理と影の面積 数学の要点まとめ 練習問題一覧




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



面積の問題 小学生 中学生 三平方の定理 みんなの算数クラブ




簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
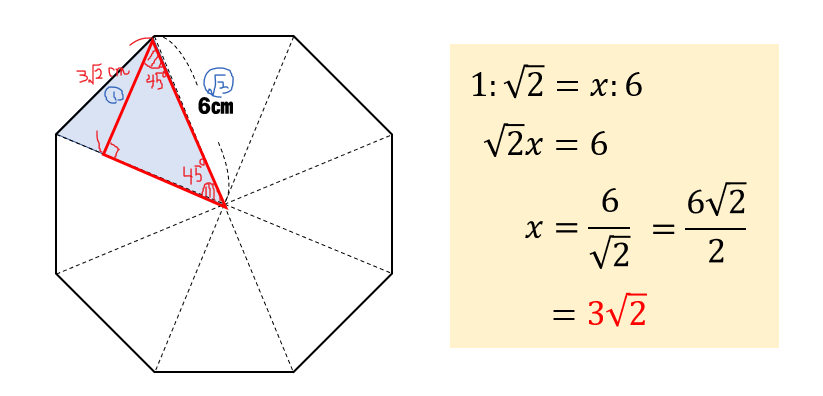



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



15年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



三平方の定理四角形の面積の求め方 下のような場合どのようにして面積を求 Yahoo 知恵袋




三平方の定理 台形の面積を求める Youtube



Studydoctor二等辺三角形や台形の面積と三平方の定理 中学3年数学 Studydoctor




三平方の定理の証明と使い方



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



平面の変換




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



Http Www Japanese Sch Ae Banner Letter Mathjournal vol 2 Pdf




中学数学 三平方の定理



ピタゴラスの定理とその証明



三平方の定理 もう一度やり直しの算数 数学




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



三平方の定理とは コトバンク
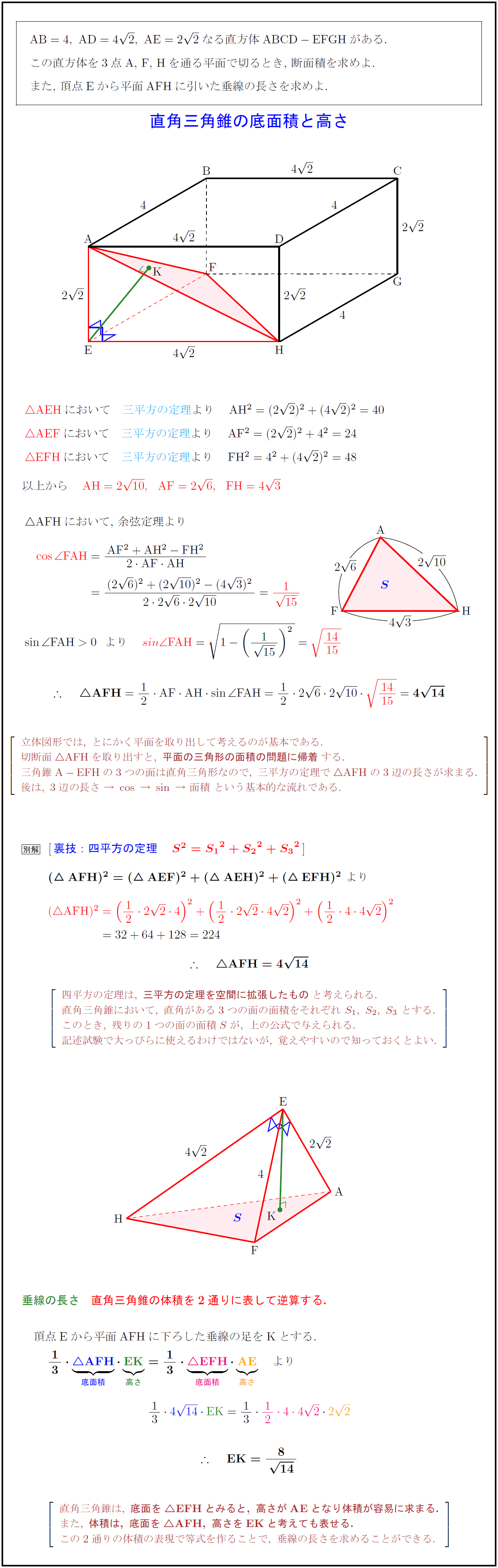



高校数学 直角三角錐 3直角四面体 の底面積と高さ 裏技 四平方の定理 受験の月




中3数学 三平方の定理16 三平方の定理と面積 円 すべて無料 星組の中学数学講座
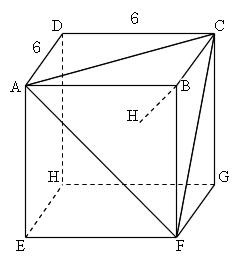



Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ



高校入試の出題分野より 三平方の定理と面積比 名古屋市北区の学習塾は思考力を育む 泰成スクール




三平方の定理の証明と使い方



3



三平方の定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



1




三平方の定理を使って面積を求める 無料で使える中学学習プリント




三平方の定理の証明と使い方



中3数学 三平方の定理17 三平方の定理と面積 円 すべて無料 星組の中学数学講座




三平方 三辺の長さから三角形の面積を求める
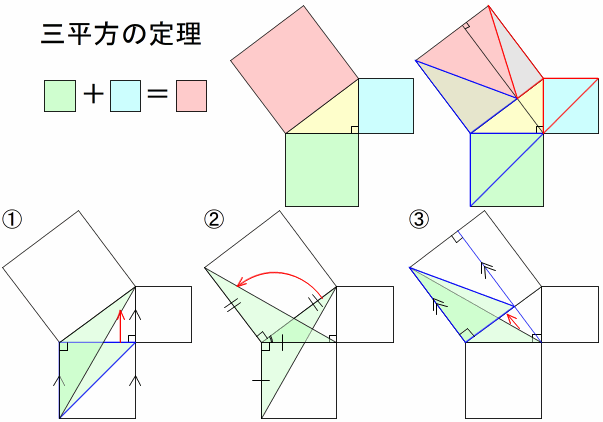



3 4 5の三角形で 本当に直角ができる Note Board




直角三角形の辺の長さ 合同条件 面積について アタリマエ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor
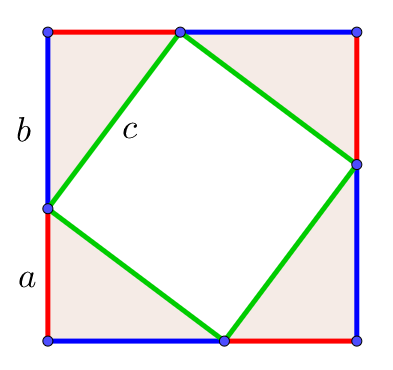



三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ




三平方の定理の証明 その3 Last Entry 第6話 Factory Takumaro ページ
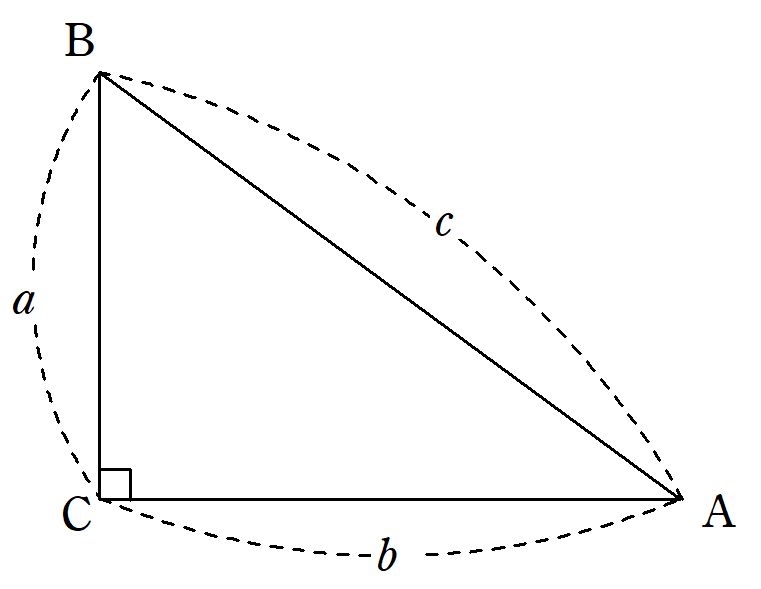



三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも
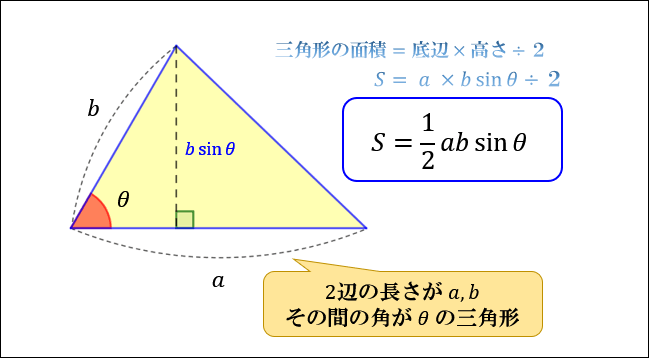



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




公文数学i教材からj教材へ 公文と小3息子の教育 日常



三平方の定理



高校入試の出題分野より 三平方の定理と面積比 名古屋市北区の学習塾は思考力を育む 泰成スクール




75 三 平方 の 定理 証明 中学生 最高のぬりえ




三平方の定理の拡張について考えよう 理科好き子供の広場




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




中学受験算数 等積変形の利用 ヒポクラテスの月
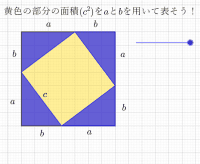



三平方の定理 Geogebra




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学



1




三平方の定理と二等辺三角形 Youtube




数学 中3 61 三平方の定理 基本編 Youtube



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



1



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション



三平方の定理の証明 直感的に分かる図で解説します 数学fun


